Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and · You have x^2y^2=(xy)(xy) So in your case (x^2y^2)/(xy)=((xy)(xy))/(xy)=xyYou can use the quadratic formula x^2 (2y)x (y^2) = 0\to \\ x= \frac{2y \pm \sqrt{4y^2 4(1)(y^2)}}{2} \\ =y \pm\sqrt{2}y = (1 \pm \sqrt{2})y So x^2 2xy y^2 = x (1\sqrt{2})yx (1\sqrt{2})y

Practice Problems 10 And 11
(x+y)^2-(x-y)^2
(x+y)^2-(x-y)^2-Solve y'2y/x=x^2y^2 Extended Keyboard;Dann hol' dir deinen persönlichen Lehrer!



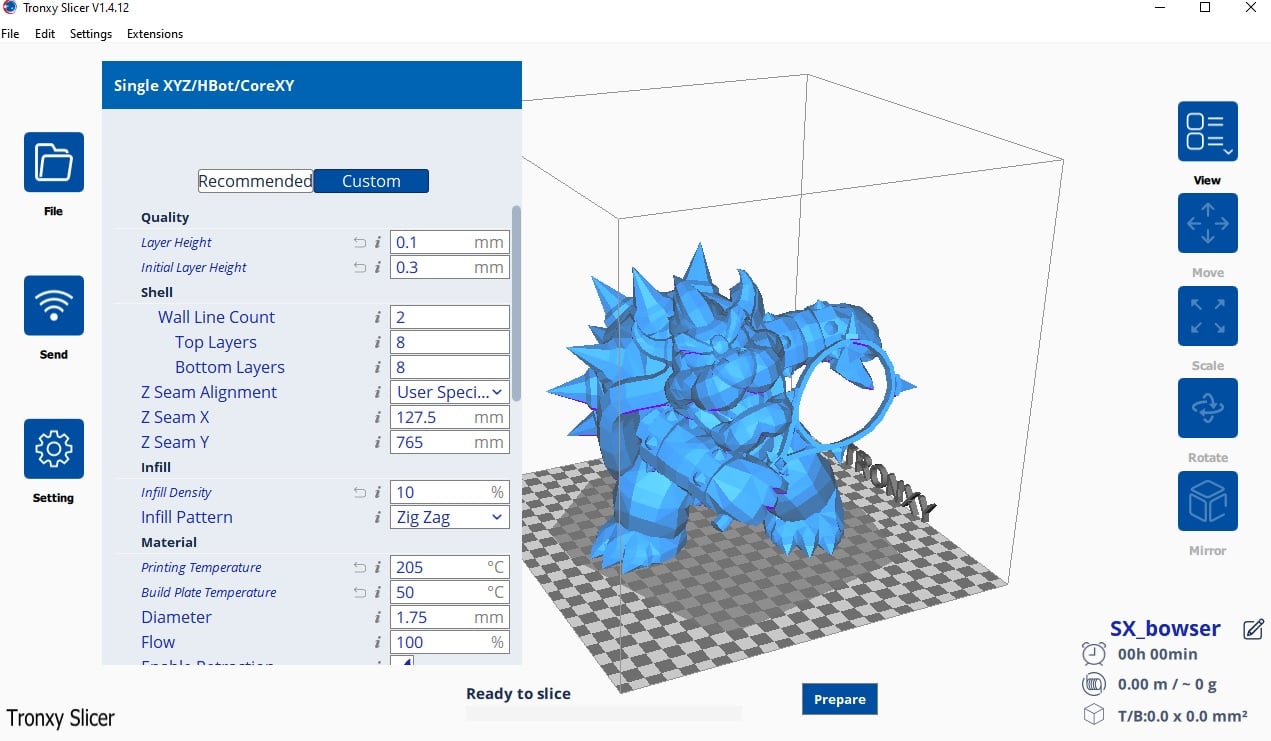
Buy Tronxy Xy 2 Pro 3d Printer 3dprintersbay
Binomischer Lehrsatz für natürliche Exponenten Für alle Elemente und eines kommutativen unitären Rings und für alle natürlichen Zahlen ∈ gilt die Gleichung () = ∑ = − ()Insbesondere gilt dies für reelle oder komplexe Zahlen und (mit der Konvention =) Die Koeffizienten dieses Polynomausdrucks sind die Binomialkoeffizienten = ⋅ (−) ⋯ (− ) ⋅ ⋯ =!Wobei B ˆ= f(x;y) 2R2 4 x2 y2 ˆ2;2 Aufgabe (a) DefiniereA n= f(x;y) 2R2 jx2y2
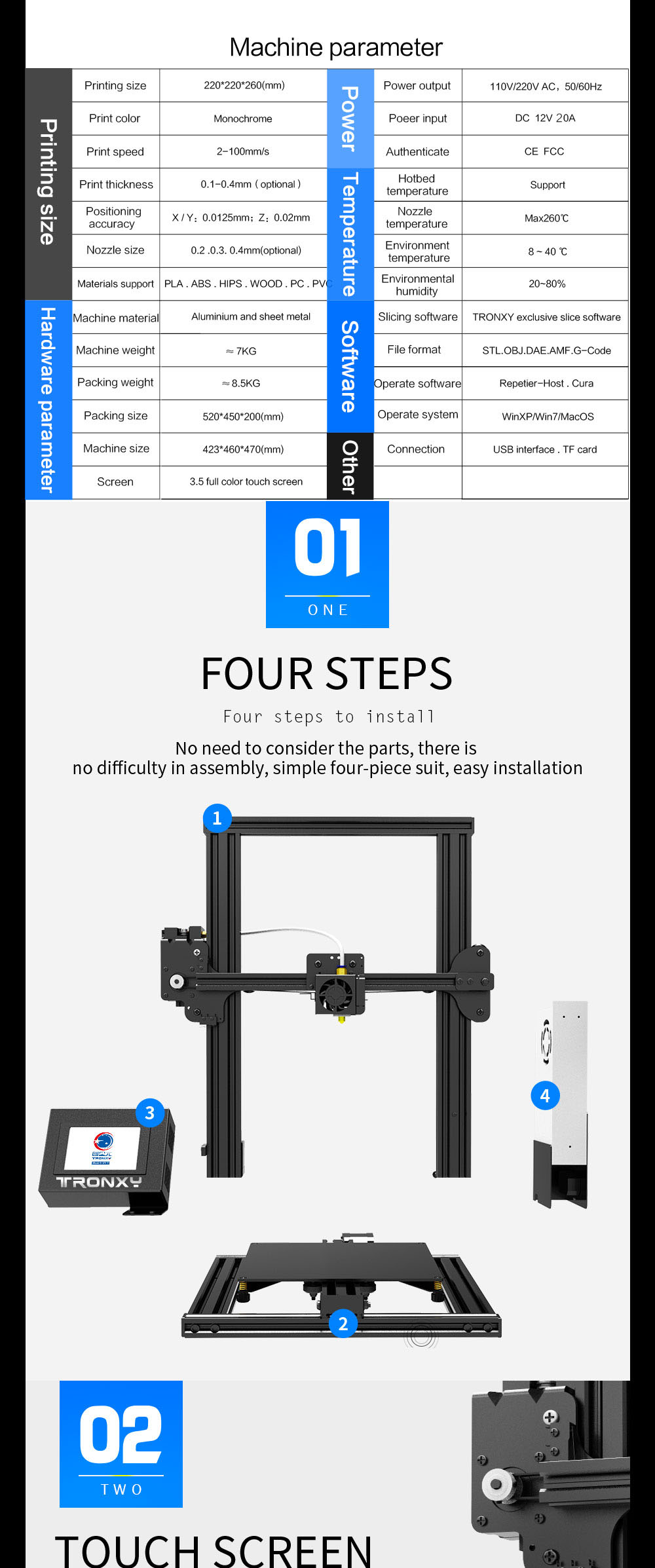
Y'=(xy)^2 mit y(0)=0 ich hab schon versucht die homogene Dgl y'2xyy^2=0 durch substituion ( z=y^1) (Bernoullische Differentialgleichung) zu lösen, hat aber nicht funktioniert da ich später e^X^2 integrieren musste Das ist glaub ich auch nicht der richtige ansatz Ich hoffe mal das mir jemand helfen kann , 1740 iammrvipX2y=4 Geometric figure Straight Line Slope = 1000/00 = 0500 xintercept = 4/1 = yintercept = 4/2 = 2/1 = 0000 Rearrange Rearrange the equation by subtracting 2x2y=4 2 x − 2 yLösen Sie Ihre Matheprobleme mit unserem kostenlosen Matheproblemlöser, der Sie Schritt für Schritt durch die Lösungen führt Unser Matheproblemlöser unterstützt grundlegende mathematische Funktionen, AlgebraVorkenntnisse, Algebra,
Ich könnte mir auch gut vorstellen, dass man an einer Stelle durch gekonntesCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyGraph x^2y^2=2y Subtract from both sides of the equation Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the right side Tap for more steps Cancel the common factor of Tap for more steps Cancel the common factor Rewrite the expression



If X Y 8 Amp X Y 2 Find The Value Of 2x 2 2y 2 Brainly In
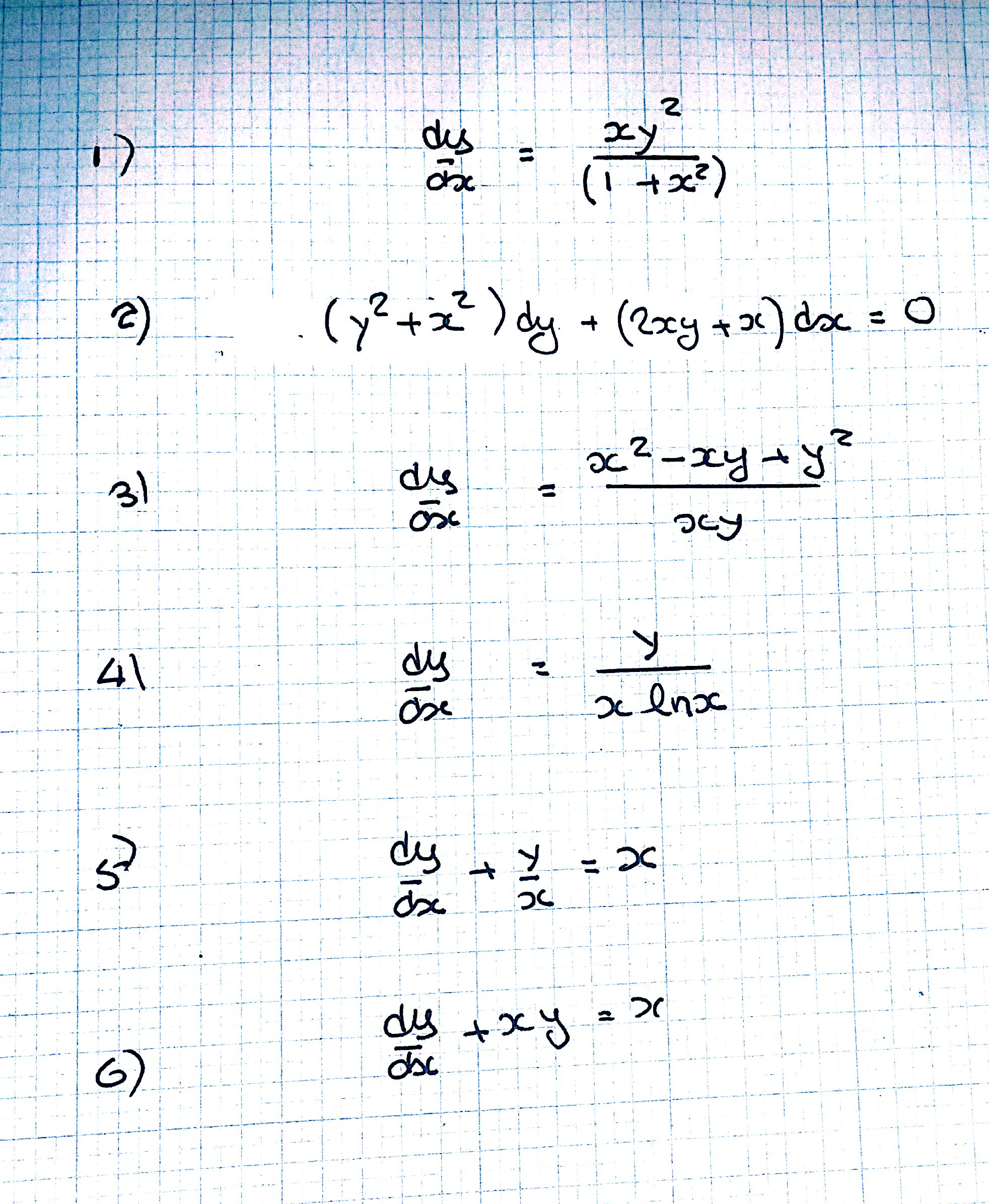


Solved Dy Dx Xy 2 1 X 2 2 Y 2 X 2 Dy 2xy Chegg Com
· The factors of y2 = (y)(y) Since the second sign is positive we are adding the factors meaning the signs of the factors need to be the same Since the first sign is negative both signs must be negative The factors are (x −y)(x − y)Aufgabe y'(x)=(y(x)x)^2 Hallo liebe Community, ich komme bei der Aufgabe einfach nicht weiter Es wäre super, wenn mir jemand weiterhelfen könnte Durch Substitution mit z=yx erhalte ich z^2=z'1 \( \int\limits_{0}^{\infty} \) dx = \( \int\limits_{0}^{\infty} \) dz/(z^21) xx 0 = 1/2 lnIz1I 1/2 lnIz1I 1/2 lnIz 01I 1/2 lnIz 0 1IPlease Subscribe here, thank you!!!



How To Find The Domain And Range Of F X Y Ln Xy 2 Math Videos F X Domain



Tronxy Upgraded Xy 2 Pro 255 X 255mm 3d Printer
Die Frage steht oben ich würd auf % tippen, aber mir hat jemand gesagt es seien 25% wodurch ich nun verunsichert binkomplette Frage anzeigen 2 Antworten Vom Fragesteller als hilfreich ausgezeichnet Maity , 1441 25% ist richtig Stell dir dasDie mathematische Funktion arctan2, auch atan2, ist eine Erweiterung der inversen Winkelfunktion Arkustangens und wie diese eine Umkehrfunktion der Winkelfunktion Tangens Sie nimmt zwei reelle Zahlen als Argumente, im Gegensatz zum normalen Arkustangens, welcher nur eine reelle Zahl zum Argument hat Damit hat sie genügend Information, um den Funktionswert in einemExample 2 y = x 2 − 2 The only difference with the first graph that I drew (y = x 2) and this one (y = x 2 − 2) is the "minus 2" The "minus 2" means that all the yvalues for the graph need to be moved down by 2 units So we just take our first curve and move it down 2 units Our new curve's vertex is at −2 on the yaxis
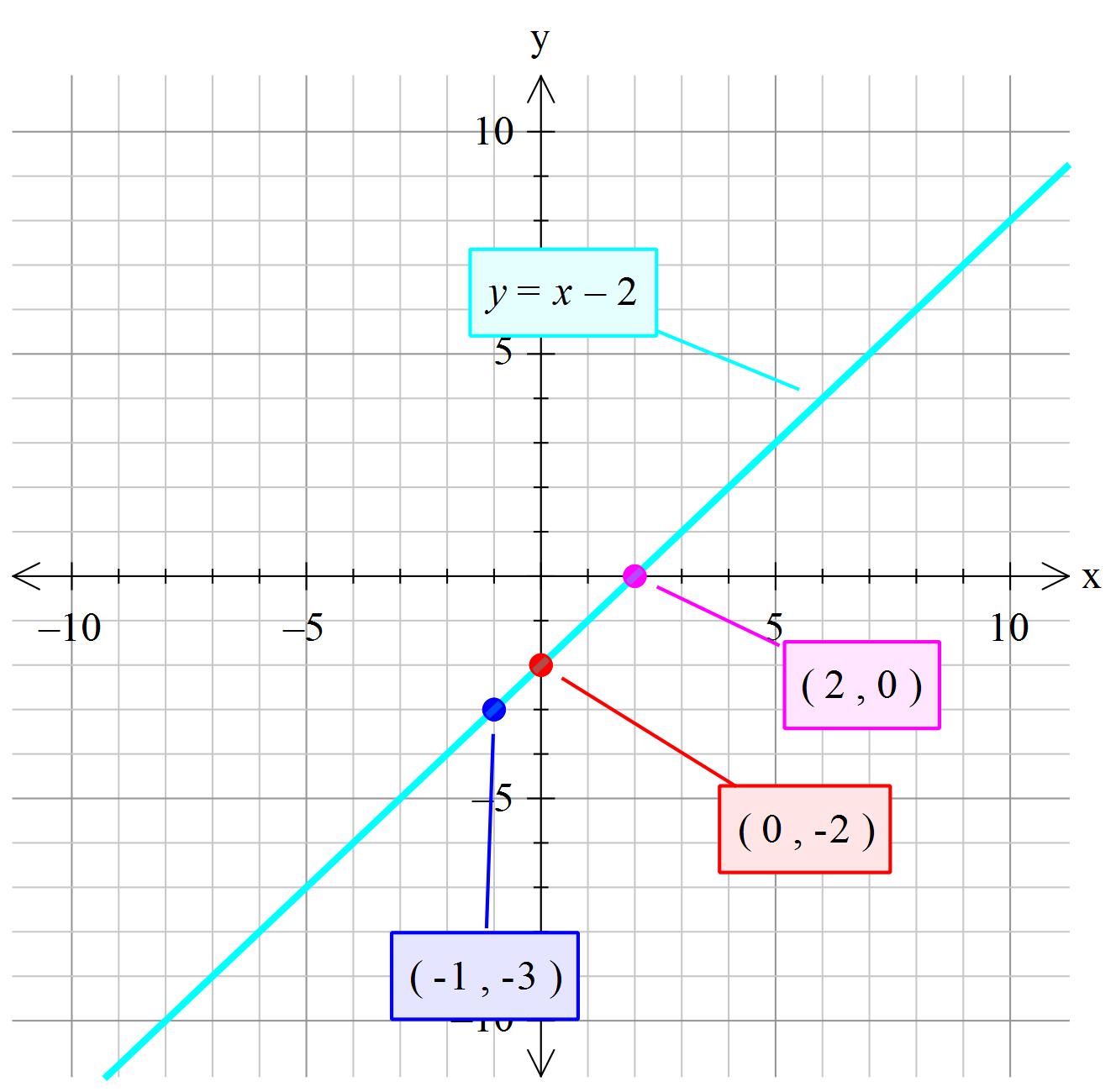


How Do You Graph The Line X Y 2 Socratic



Ex 6 2 5 Solve X Y 2 Graphically Chapter 6 Cbse
· exp ( x ; · 2 Variablen x & Y sind indirekt proportional zueinander Um wieviel Prozent ändert sich x wenn y um % abnimmt?Simplify (xy)^2 Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more steps Multiply by Rewrite using the commutative property of multiplication Multiply by Multiply by Multiply by



File X Y 2 Svg Wikimedia Commons



Solve By Substitution X 2 Y Xy 2 30 X Xy Y 11 Please Answer Soon Brainly In
Subtract x^ {2} from both sides of the equation Subtracting x^ {2} from itself leaves 0 Divide x, the coefficient of the x term, by 2 to get \frac {x} {2} Then add the square of \frac {x} {2} to both sides of the equation This step makes the left hand side of the equation a perfect square Square \frac {x} {2}Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations (xy)2(xy)2=4xy so that you understand betterOnlineBerechnung mit der Funktion vereinfachen des Ausdrucks vereinfachen(x*x2*xx)



Hjc Youth Cl Xy 2 Helmet Solid 10 9 50 Off Revzilla



Xy 2 Pioneer Pro Audio
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `x(1y^2)dxy(1x^2) dy=0`Graph x=y^22y1 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the right side Tap for more steps Cancel the common factorX^3 x^2 y x y^2 y^3 Extended Keyboard;


Solved W F X Y Z Xy 2 Z 3 3yz Compute I W X Chegg Com



X Y 2 3 Find The Expansion Of The Following Brainly In
This is always true with real numbers, but not always for imaginary numbers We have ( x y) 2 = ( x y) ( x y) = x y x y = x x y y = x 2 × y 2 (xy)^2= (xy) (xy)=x {\color {#D61F06} {yx}} y=x {\color {#D61F06} {xy}}y=x^2 \times y^2\ _\square (xy)2 = (xy)(xy) = xyxy = xxyy = x2 ×y2Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyGraph x^2y^2=1 Find the standard form of the hyperbola Tap for more steps Flip the sign on each term of the equation so the term on the right side is positive Simplify each term in the equation in order to set the right side equal to The standard form of an ellipse or hyperbola requires the right side of the equation be This is the form of a hyperbola Use this form to



Buy Tronxy Xy 2 Pro 3d Printer 3dprintersbay



19 Tronxy Xy 2 Pro Assembled Upgraded High Precision Resume Print 3d Printer 3d Printers 3d Printers Supplies
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and · ich soll zeigen, dass ^$${ e }^{ \frac { xy }{ 2 } }\le \frac { { e }^{ x }{ e }^{ y } }{ 2 } x,y∈ℝ $$ gilt Mein Ansatz war durch umformen einen eindeutigen Ausdruck zubekommen nur mein Letzter logischer Term lautet (e^xe^2)*(e^ye^2) = e^x/2e^y/2 Hat einer eine Idee wie es da weiter geht ?Keines Wegs hatte ich ja nach x oder y aufgelöst Wenn ich diese eFunktion raus schmeiße, kann ich weiter nichts hoffen, als eine notwendige Kurve oder Punkte zu kriegen, wo sich die Lösung höchstens aufhalten



Factorlse 25 X Y 2 36 X 2 Y 2



Renault Project Xy 2 Can Fit Two But They Won T See Or Be Seen Carscoops
· Gegeben ist die Funktion f(x,y)=\( \frac{x*y^2}{x^2y^4} \) (X;Y) ungleich (0;0) Soll vielleicht F( dank schonmal f(x,y) = (xy^2)/(x^2 y^4) dank schonmal f(x,y) = (xy^2)/(x^2 yY ) = quadr Ausdr 2 ( x ;Consider x^{2}y^{2}xy22xy as a polynomial over variable x \left(xy1\right)\left(xy2\right) Find one factor of the form x^{k}m, where x^{k} divides the monomial with the highest power x^{2} and m divides the constant factor y^{2}y2 One such factor is xy1 Factor the polynomial by dividing it by this factor Examples Quadratic equation { x } ^ { 2 } 4 x 5 = 0 x 2 − 4 x



Solve The Following Pairs Of Linear Equation 3 X Y 2 X Y 3 2 X Y 3 X Y 11 3 Brainly In


How To Solve 3x Xy 2 Dx X 3 2y Dy 0 Quora
//googl/JQ8NysMy TA did this one, using a different method Hope this helps(x;y;z) 2R3 jz= x2 y2;0 z 4, H= n (x;y;z) 2R3 jz= p 1 x2 y2;1 z 5 o, K= n (x;y;z) 2R3 jz= p x2 y2;0 z 4 o a)Alle drei Flaschen haben Höhe 4 vom Boden der Flasche aus gemessen Welche fasstammeistenWasser,wennmansiebiszumRandfüllt?Y ) exp ( x ;



Given X 2 Y 2 74 And Xy 35 Find The Value Of X Y And X Y
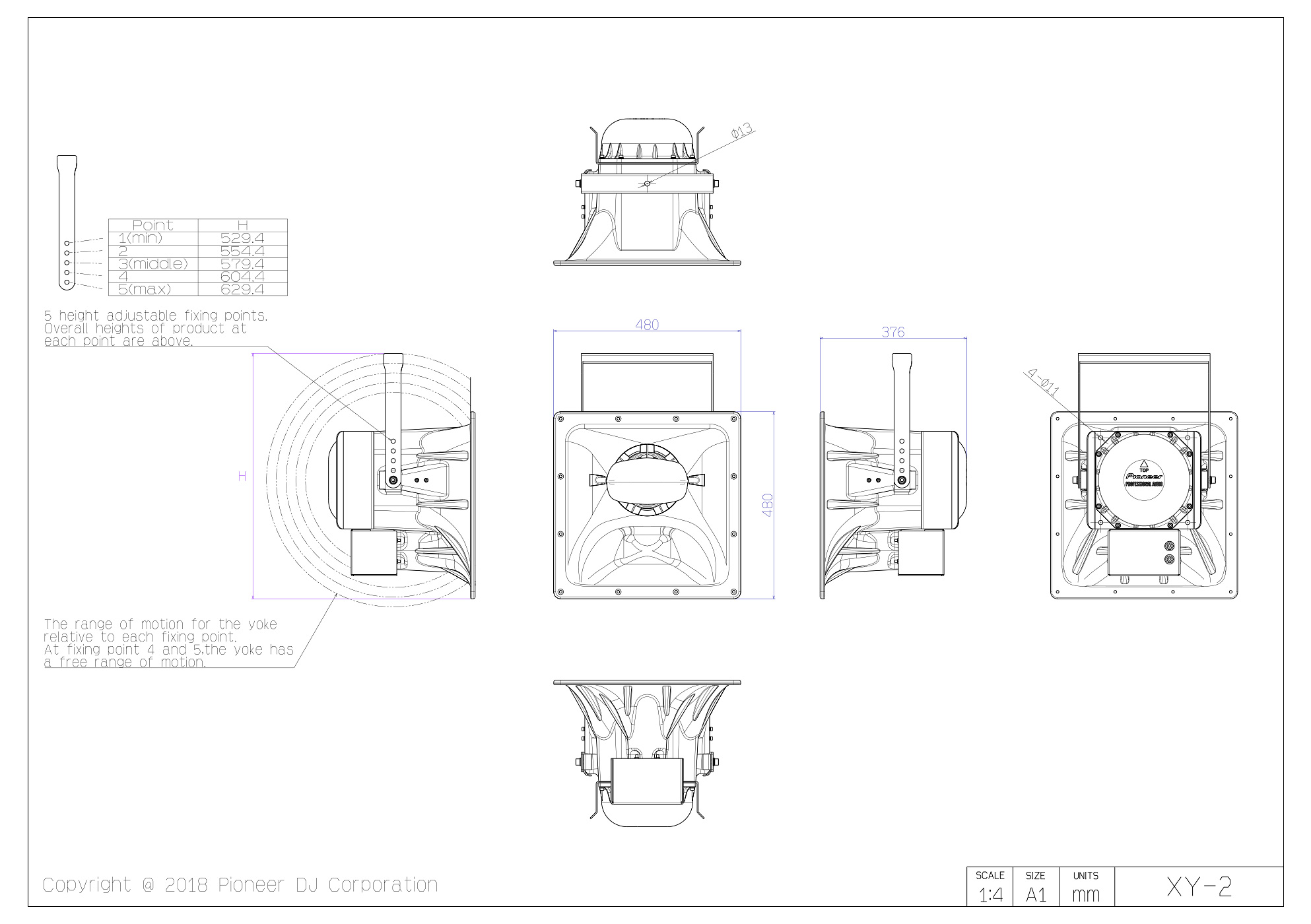


Xy 2 Pioneer Pro Audio
We have x^2y^2=36z^2 and xy=10z, which gives (10z)^22xy=36z^2 or xy=3210zz^2 and xyz=32z10z^2z^3 Also, (xy)^2\geq4xy, which gives 3z^2z28\leq0 or 2\leq z\leq\frac{14}{3} Also, (xy)^2\geq4xy, which gives 3z^2z28\leq0 or 2\leq z\leq\frac{14}{3}The focus of a parabola can be found by adding to the xcoordinate if the parabola opens left or right Substitute the known values of , , and into the formula and simplify Find the axis of symmetry by finding the line that passes through the vertex and the focus Find the directrix Tap for more steps The directrix of a parabola is the vertical line found by subtracting from the xY ) = quadr Ausdr 1 ( x ;



Hjc Cl Xy Ii Ellusion Youth Helmet Xtremehelmets Com



Renault Project Xy 2 On Behance
Y=2(x 3) 6 y= 2x66 y=2x66 y=2x y=2x x= y/2 Mehr anzeigen Nachhilfe mit DurchkommGarantie Nur erfahrene Lehrer Alle Fächer Gratis Probestunde Jetzt anfragen Die besten 11 Lehrer Du brauchst zusätzliche Hilfe?Find the solution of the differential equation that satisfies the given initial conditionxy' y = y^2, y(1) = 1Wenn bei der partiellen Ableitung von x y=0 ist, dann ist die Funktion immer 0 bei y=x^2 läuft der Funktionswert gegen unendlich bei x gegen 0 Aber die Funktion ist ja definiert durch wenn (x,y)=0 dann nutze 0 als Funktionswert Bei y=x^2 und x=0 wird einfach null genutzt Und stetig ist es auch, weil wenn man eine Nullfolge einsetzt kommt



How Do You Differentiate 1 X Sin Xy 2 Socratic



Please Quickly Answer Factorise 2x 3 Xy 2 Y 3 Maths Polynomials Meritnation Com
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge andAlle anzeigen Lars Nolden, 31 Mathe Statistik Ausbildung Ich bin wie ihr alle in der GrundschuleY ) So würde man also keine Gleichung umstellen;



Factorise Using Identities 16 X Y 2 81 X 2y 2 Maths Factorisation Meritnation Com



Find The Area Of The Shaded Region X Y 2 1 Y 1 X Sqrt Y Mathematics Stack Exchange
Lösung Wir berechnen jeweils zuerst das Volumen zwischen der Flaschenoberfläche und der xyEbene Beachte, dass das das VolumenBeispiele 1) x2 3y – sin(x) y' 35 (y'')2 = 0 DGL 2 Ordnung 2a) y' = y b) y' = ky DGL 1 Ordnung 3) y'' = g = konstant DGL 2 Ordnung 4) N(t) = k N(t) DGL 1 Ordnung Wir betrachten zuerst Differentialgleichungen 1 Ordnung und gehen davon aus, dass die Gleichung F(x,y,y') = 0 nach y' aufgelöst werden kann, dh es gilt y' = g(x,y) 1 Trennung (Separation) derSimple and best practice solution for x^2y^2= equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it Equation SOLVE Solution for x^2y^2= equation Simplifying x 2 y 2



Practice Problems 10 And 11
.jpg)


Xy 2 Pro Shenzhen Tronxy Technology Co Ltd
X^ {2}2yxy^ {2}=0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x=\frac {2y±\sqrt {\left (2y\right)^ {2}4y^ {2}}} {2}0 y xgfur ˆ>2 L osungsvorschlag zu a) (i) Wir verwenden Polarkoordinaten und erhalten mit derX2 y2 d(x;y;z), wobei er Bereich sei, welcher von dem durch z= x 2 y beschriebenen Paraboloid und der durch z= 1 gegebenen Ebene begrenzt wird c) Berechnen Sie lim ˆ!1 Z Bˆ x y (x3 x2y xy2 y3)(ln(x2 y2))2 d(x;y);



Tronxy Xy 2 Pro Titan Pro 2e Upgrade Kit Package For Xy 2 Pro Titan Upgrade To Xy 2 Pro 2e



The Solution Of The Equation X Y 2 And X Y 4 Is Brainly In
· x / y y / x > 2 Erweitern, auf einen Nenner bringen x^2 /( xy) y^2 / (xy) > 2 ( x^2 y^2 ) / ( x * y ) > 2 Im Zähler steht immer etwas positives Im Nenner steht bei einer positiven und einer negativen Variablen etwas negatives, also ist der ganze Bruch negativ und somit Tronxy Xy 2 Pro 3d Printer Unbox Setup Youtube One Of The Factor Of X Y 2 4 X Y 45 Is Maths Algebraic Identities And Factorisation Meritnation Com Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and capabilities to the broadest possibleAll equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}yxy^ {2}=4 x 2 y x y 2 = 4 Subtract 4 from both sides of the equation · Auf der Menge R R sei eine Relation gegeben durch (x1, y1) R (x2, y2) x12y12= x22y22 Zeigen Sie, dass eine Äquivalenzrelation ist und skizzieren Sie die Äquivalenzklasse von ( Kommentiert 5 Nov 16 von abcdefg1234 a) Auf der Menge R × R sei eine Relation ∼ gegeben durch (x1,y1) ∼ (x2,y2) ⇐⇒ x12 y21 = x2 y2 If X 2 Y 2 29 A N D X Y 2 Find The Value Of Z Xy 2 Geogebra Tronxy Xy 2 Has Failed Me Again The Heatbed Temp Had Glitched And Everything Else Gone Wild 3dprinting Layer Shifting Tronxy Xy 2 Problem Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange Worked Example Implicit Differentiation Video Khan Academy Find The Asymptotes Of The Following Curves Y 3 3x 2y X Y 2 3x 3 2y 2 2x Y 4x 5y 6 0 Youtube Hawon Jang Renault Project Xy 2 Draw The Graph Of X Y 2 Please I Need Answer Brainly In Solved Consider The Curve Given By The Equation Y 3 Xy Chegg Com Tronxy Xy 2 Pro 3d Printer Print Size 255x255x260mm With Removable Build Surface Plate Resume Printing Function After Power Off Filament Detection Automatic Leveling Amazon Com Industrial Scientific Solved Solve The Differential Equation Dy Dx Xy 2 1 Chegg Com Pokemon X Y Vol 2 2 Kusaka Hidenori Yamamoto Satoshi Amazon Com Books X Y 2 Dy Dx A 2 X Y U Youtube Fully Autonomous Renault Project Xy 2 Has No Windows And Is Designed For Blind Dates Techeblog Tronxy Xy 2 Pro User S Manual Installation Manual Pdf Download Manualslib Tronxy Xy 2 Pro Review Hands On All3dp Tronxy Xy 2 Pro 3d Printer Review The Specs 3d Prints Solve The Differential Equation X Y 2 X Dx Y X 2 Y Buy Tronxy Xy 2 Pro 3d Printer Kit 3d Printers Online Store 127 With Coupon For Tronxy Xy 2 Pro 3d Printer Kit Germany Warehouse From Tomtop China Secret Shopping Deals And Coupons Solved Consider The Function F X Y Xy X 2 Y 2 Chegg Com Buy Tronxy Xy 2 3d Printer Kit 3d Printers Online Store How To Solve The Ordinary Differential Equation X 2 Y 2 X Y 2y X 4 Mathrm E X Mathematics Stack Exchange Max And Min X Y Ln X 2 Y 2 Mathematics Stack Exchange If X Y 2 And 2 X Y 1 5 Then Find The Value Of X And Y Brainly In Tronxy Xy 2 Pro 3d Printer Electronics Others On Carousell Find X Y Z From The Following Equation X Y 2 5 Z Xy 6 2 5 8 Youtube Bijection Function F X Y X Y 1 2x 2y 2 Mathematics Stack Exchange Solved Solve The Differential Equation X Xy 2 Dx E X Chegg Com Solve 3 X Y 2 X Y 2 And 9 X Y 1 Brainly In Buy Tronxy Xy 2 Pro Titan Extruder 3d Printer For Just 9 99 The Factors Of X 3 X 2y X Y 2 Y 3 Are A X Y X 2 X Y Y 2 B X Y X 2 X Y Y 2 C Youtube Tronxy Upgraded Xy 2 Pro 255 X 255mm 3d Printer How Do You Solve The System X Y 6 And X Y 2 By Graphing Socratic Solved A Picture Of The Function F X Y X 3y Xy 3 X Chegg Com Buy Tronxy Xy 2 Pro 3d Printer Kit 3d Printers Online Store Tronxy Xy 2 Aluminum 3d Printer Tronxy Xy 2 Pro 3d Printer Kit 255x255x260mm 3d Printer Kit Printer 3d Printer Silent Mainboard With Wire Cable For What Value Of N Is Following A Homogeneous Differential Equation Renault Project Xy 2 By Hawon Jang Motivezine How Do You Solve X Y 4 And X Y 2 By Graphing Socratic How Do You Implicitly Differentiate 2 E Xy 2 Xy Y 2x 3 Y Socratic Marley Firmware For Tronxy Xy 2 And Xy 2 Pro General Tronxy Xy2 Pro Groups Thingiverse 0 3d Printer With Auto Bed Leveling Review Of The Tronxy Xy 2 Pro 3d Printer 3dprintlove Tronxy 255x255x260mm Xy 2 Pro 24v Quick Install 3d Printer 3 5inch Full Color Touch Screen Sale Price Reviews Gearbest Renault Project Xy 2 On Behance How Do You Do Implicit Differentiation For X 2y 2 Xy 2 Socratic How Do You Differentiate Xy 2 Xy 12 Socratic The Solution Of The Differential Equation Y Xy 2x 2y 2 Dx X Xy X 2y 2 Dy 0 Is Given Youtube Hjc Cl Xy 2 Batman Motorcycle Helmet Richmond Honda House Tronxy Xy 2 Pro Titan Extruder Can Print Ptu Tronxy New Design Fast Assembly Xy 2 Pro With Auto Leveling 3 5 Inch Touch Screen 3d Printers Aliexpress Tronxy 3d Printer Parts X5sa Series Xy 2 Xy 3 Silent Mainboard 3d Printer Accessories Motherboard For 3d Ducker Imptesoras 3d Printer Parts Accessories Aliexpress Tronxy Xy 2 Pro Titan Pro 2e Upgrade Kit Package For Xy 2 Pro Titan Upgrade To Xy 2 Pro 2e If X Y 3 And Xy 2 Then The Value Of X 3 Y 3 Is Equal To Brainly In X Y Is The Solution Of The Given Simultaneous Equc Practice Set 1 4 Solve The Following Simultaneous Equations 2 3 77 X Y X Y 10 2 15 T 4 5 X Y 2 X Y X Y X Y 27 31 31 27 3 85 2 Y 3 X 2 Y 3 1 1 3 1 1 1 Factorization Of The Polynomial X Y 2 A 2 2 X Y X Y Ab B 2 X Y 2 Gives Youtube Newest Version Xy 2 X5sa 3d Printer Mainboard With Wifi Module Upgrades Controller Board 32bit Motherboard Factorise X Y 2 7 X 2 Y 2 12 X Y 2 Youtube Raptor Z Xy 2 Heavy Springs Custom Easy Answered 7 Y 9 Xy Y Vx 11 Xy 2y X X 0 Bartleby Speaker Xy 2 Pioneer Pro Audio Tronxy Xy 2 Pro Titan Extruder Can Print Ptu Tronxy New Design Fast Assembly Xy 2 Pro With Auto Leveling 3 5 Inch Touch Screen 3d Printers Aliexpress Solve X Y 14 X Y 2 Tronxy Xy 2 Pro Review Hands On All3dp






































































































































































































0 件のコメント:
コメントを投稿